
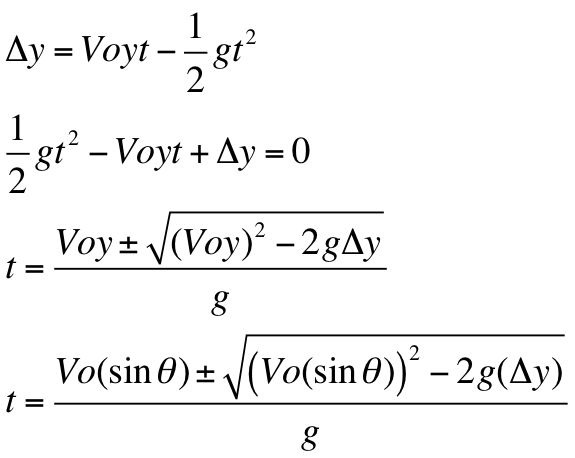
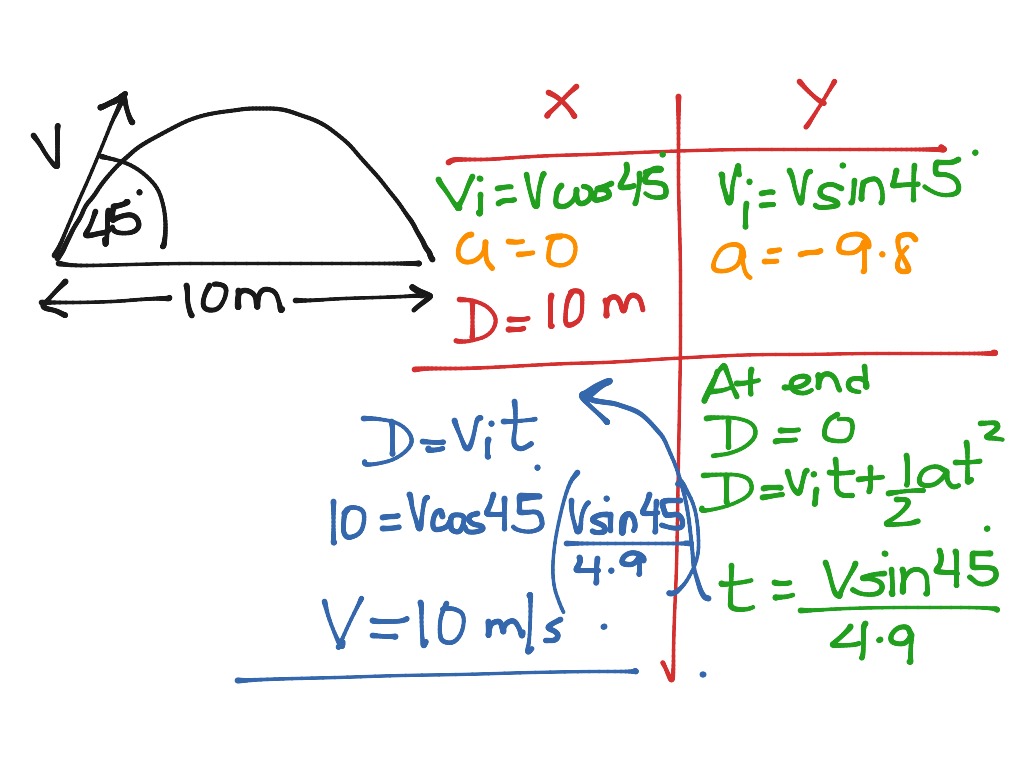
In the following, we ignore the effect of air resistance. In particular, let’s consider the effect of gravity on the motion of an object as it travels through the air, and how it determines the resulting trajectory of that object. Now let’s look at an application of vector functions. The acceleration vector points toward the inside of the turn at all times. Using measurements of the earth's mass and radius, as well as Newton's constant of gravitation, we can determine that the average value of a on the Earth's surface is about 9.\): The dashed line represents the trajectory of an object (a car, for example). We can plug this in for the attraction force, giving us this:Ĭanceling out m2, we get a definition for gravitational acceleration:įrom here, we have to use measurements to help us. So, the mass on the left side of the following equation would refer to the person, which we can arbitrarily call m2. Here, we are looking for the force on the person from the earth. If we take this equation and frame it in terms of somebody standing on the earth, we get a force due to gravitational attraction that is the product of their masses divided by the square of the earth's radius.įrom here, we can take Newton's second law of motion, f = ma. If you look at Newton's law of universal gravitation, you see that the force of attraction between two objects is proportional to the product of their masses and inversely proportional to the square of the distance between them. A heavier object has more inertia, which is a resistance to a change in motion. While it's true that there is more gravitational force acting on a heavier object, this doesn't correspond to an increase in acceleration.

In order to make this equation more universal, the position equation can be generalized as x(t) = 1/2(at^2) + v_0 + x_0 Simplifying the integral results in the position equation x(t) = -4.9t^2 + (C_1)t + C_2, where C_1 is the initial velocity and C_2 is the initial position (in physics, C_2 is usually represented by x_0). Position is the antiderivative of velocity, so that means that x'(t) = v(t) and x(t) = int. To find the position equation, simply repeat this step with velocity. This means that for every second, the velocity decreases by -9.8 m/s. time graphs for both the horizontal and vertical components of the projectiles. Simplifying the integral results in the equation v(t) = -9.8t + C_1, where C_1 is the initial velocity (in physics, this the initial velocity is v_0). Determine the best fit equations for the position vs. We can use this knowledge (and our knowledge of integrals) to derive the kinematics equations.įirst, we need to establish that acceleration is represented by the equation a(t) = -9.8.īecause velocity is the antiderivative of acceleration, that means that v'(t) = a(t) and v(t) = int. We know that acceleration is approximately -9.8 m/s^2 (we're just going to use -9.8 so the math is easier) and we know that acceleration is the derivative of velocity, which is the derivative of position. We usually start with acceleration to derive the kinematic equations.
#ADVANCED PROJECTILE MOTION EQUATIONS PLUS#
3 m/s ) 2 − 4 t, equals, start fraction, minus, 18, point, 3, start text, space, m, slash, s, end text, plus minus, square root of, left parenthesis, 18, point, 3, start text, space, m, slash, s, end text, right parenthesis, squared, minus, 4, open bracket, start fraction, 1, divided by, 2, end fraction, left parenthesis, minus, 9, point, 81, start fraction, start text, space, m, end text, divided by, start text, space, s, end text, squared, end fraction, right parenthesis, left parenthesis, minus, 12, point, 2, start text, space, m, end text, right parenthesis, close bracket, end square root, divided by, 2, open bracket, start fraction, 1, divided by, 2, end fraction, left parenthesis, minus, 9, point, 81, start fraction, start text, space, m, end text, divided by, start text, space, s, end text, squared, end fraction, right parenthesis, close bracket, end fraction For instance, say we knew a book on the ground was kicked forward with an initial velocity of v 0 = 5 m/s v_0=5\text t = 2 − 1 8.


 0 kommentar(er)
0 kommentar(er)
